In my recent posts on evaluating benchtop NMR system performance, I discussed the fundamental role the static (B0) magnetic field homogeneity plays in defining the lineshape and with it the resolution performance of the instrument. However, the quality of the magnetic field affects much more than just the instrument’s lineshape and resolution: since broadening of the lines due to B0 inhomogeneity causes them to be lower in amplitude, the quality of the field also directly affects the instrument’s sensitivity. In this post I explore the concept of instrument sensitivity in more detail and look at how to measure 1H sensitivity.
What is Meant by Sensitivity?
A formal definition of sensitivity is the ability of an instrument to detect a target analyte. This is usually expressed in NMR as the signal-to-noise ratio (SNR) for a defined concentration of reference substance. Simply put, the more sensitive the NMR spectrometer, the less sample you need to get the same SNR in your spectrum. The two principal enemies of any analytical measurement are higher noise levels and a lower intensity of the signal measured by the instrument’s detector for a sample of given concentration. With modern electronics the noise levels are consistent and should not vary much between different instruments. This means the sensitivity depends primarily on the signal amplitude, which in turn depends on the lineshape and resolution of the instrument. A poor lineshape results in spectra with broad lines that are lower in amplitude, which decreases the SNR, thereby degrading the sensitivity of the instrument and increasing the amount of sample and/or measurement time required to get the same SNR in the spectrum, as we will see below.
Signal Averaging and Signal-to-Noise in NMR
One of the simplest ways to improve the SNR of any NMR measurement is to do what we call signal averaging. Signal averaging consists of repeating the measurement (the “scan”) several times and co-adding the signal from each measurement. This improves the SNR because the signal intensities increase in proportion to the number of scans, while the noise due to its random nature increases more slowly, in proportion to the square root of the number of scans. Hence, the SNR of an NMR measurement increases in proportion to the square root of the number of scans
SNRN = SNR1 x N1/2 [1]
where N is the number of scans, SNR1 is the SNR obtained in a single scan and SNRN is the SNR obtained in N scans. So, a 4-scan measurement will have double the SNR of a single-scan one, a 16-scan measurement will show a four-fold increase in SNR, and so on. Another way to look at this is that an NMR instrument that is x (e.g. ¼) as sensitive will require a total measurement time that is x2 (e.g. 16) times longer to overcome that loss in sensitivity. The importance of the square root in the above equation cannot be overstated, as it has enormous implications for NMR measurements, as we shall see in my next post.
Standard Method for Measuring 1H Sensitivity
The way to assess an NMR instrument’s sensitivity is to collect the spectrum of a sample of known concentration and then determine the root-mean-square (RMS) noise with respect to the intensity of a specific signal in the spectrum. For benchtop 1H NMR, the convention is to use a sample of 1% (v/v) ethylbenzene in CDCl3 and to measure the SNR of the largest peak in the methylene signal (quartet) with respect to the noise in a region of the spectrum without any NMR signals.1 Certified reference samples appropriate for benchtop NMR systems are widely available (see here for example: https://www.sigmaaldrich.com/catalog/product/aldrich/717959).
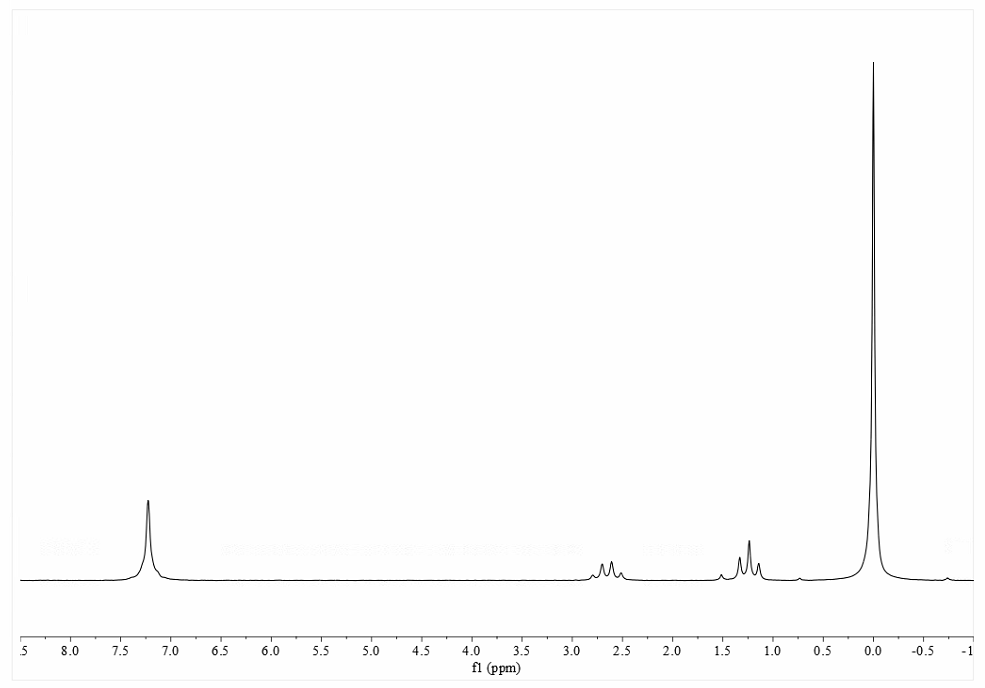
Figure 1 shows an 80 MHz 1H spectrum of the 1% ethylbenzene sample, collected using the parameters shown in Table 1.
Figure 1. 80 MHz 1H NMR spectrum of the 1% ethylbenzene sample
| Parameter | Value |
| Sample | 1% ethylbenzene in CDCl3 + 0.1% TMS |
| Experiment protocol | 1D proton (pulse-acquire) |
| Pulse flip angle | 90 degrees |
| Acquisition time | > 1 s |
| Relaxation delay | > 60 s |
| Number of scans | 1 |
| Resolution enhancement | Not used / not allowed |
| Line broadening | 1.0 Hz exponential |
Table 1. Acquisition parameters for 1H sensitivity test
The ethylbenzene test measures the SNR with respect to the methylene “quartet” signal found at around 2.65 ppm in the spectrum. It is a mistake to use the aromatic peaks around 7 ppm as this will provide a false SNR measurement that is around 5 times higher. As with all NMR measurements, the SNR in the spectrum will depend very heavily on the data processing used and, in particular, the apodization (“line broadening”) applied. (The meaning of apodization and its use in NMR are beyond the scope of this article but interested readers are directed to Ref 2.) For this test, the data should be processed using 1 Hz of exponential line broadening (the accepted standard) and, as with the 1H lineshape test, no post-processing enhancement of the signal.
When measuring the SNR, it is important to use a noise region that is wide enough to provide a statistically meaningful estimate of the noise level and one that is not at the edges of the spectrum where the noise may be attenuated by the filters used in the instrument’s receiver system. It is typical for benchtop NMR systems to use a noise region between the methylene signal and aromatic signals at around 7 ppm. There are a number of tools in standard NMR data processing software packages for determining the RMS SNR in an NMR spectrum and in this particular example we used a script in the widely used Mnova software package. Figure 2 shows the SNR calculated with respect to the methylene signal calculated using this script.
Figure 2. 80 MHz 1H sensitivity determination on 1% ethylbenzene spectrum using script in Mnova software. The reported SNR for the tallest peak of the methylene quartet is 206:1.
References
- “Nuclear Magnetic Resonance Spectroscopy”, USP-NF Chapter 761.
- “High-Resolution Techniques in Organic Chemistry”, (3rd), T.D.W. Claridge, Elsevier (2016).